Going to Mars?

A vast literature already exists on this topic, so this will be brief, and address one subject, non-Hohman transfer orbits, which can often get neglected in non-specialist publications. A Hohman transfer orbit is an ideal ellipse that is tangential to both the departure orbit and the destination orbit. A rocket is fired in line with the spacecraft's motion to put a spacecraft onto the transfer ellipse, the spacecraft coasts on the transfer ellipse to its target orbit, and another in line rocket firing puts the spacecraft in the target orbit.

For most situations, the Hohmann transfer requires the least amount of velocity change (∆v) for a given orbit transfer, and takes the most time. While eccentric orbits and launch window requirements take mission planners away from the classic Hohmann, if time is not of the essence and payload mass is at a premium, a close approximation of the Hohmann transfer has been used. The time of flight numbers one sees in many general accounts and even some basic astronautical engineering texts are Hohman transfer times.

What is sometimes left out is that for a little more ∆v, one can save a lot of time. This, of course, is not news to professional mission planners, and an alert observer will have noticed that real spacecraft take considerably less time to get to Mars than the published Hohman transfer times.



figure 1. Transfer Orbits

This is particularly true if they are headed directly for the Martian surface, and use the Martian atmosphere to take care of the difference between the spacecraft velocity vector and that of Mars. This is known variously as aerobraking or aerocapture.

While the surface pressure of the Martian atmosphere is generally something under 1% of Earth's, it is somewhat more distended and, being mostly carbon dioxide, denser at a given temperature and pressure. It thus ends up that atmospheric entry, where meteors and heatshields glow, occurs at similar altitudes on both planets--high above most relevant topography. Oh, in some three sigma scenarios with a low area to mass ratio on the entry vehicle and the Martian atmosphere in a cold, contracted state, Olympus Mons or another Tharsis volcano might come into play, but it's easy enough to use midcourse maneuvers to schedule the arrival time to avoid them.

Entry altitude at Mars is more variable than at Earth, so a good weather report and some real time trajectory management is warranted. That's not a show stopper. Some have argued that entry velocities of ten to twelve km/s are too risky and difficult to manage with crews aboard, apparently forgetting that nine manned spacecraft have returned from the Moon to enter the Earth's atmosphere at just such velocities.

What hasn't been done yet is for a spacecraft to dump enough velocity into a planet's atmosphere for capture, then skip back out again and, with a small periapsis-raising burn, go into orbit. There's nothing technically impossible about this, but it necessarily requires some sophisticated automated flying, a complexity which is more than mission planners and engineers have been willing to tackle to date. With the targeting accuracy achieved by Pathfinder and the other rovers, perhaps confidence has been gained.

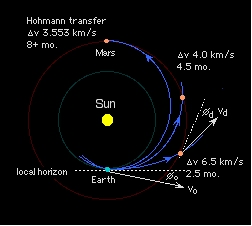
If we can use the Martian atmosphere for the second ∆v, and then make propellants for the return trip from Martian resources, the Mars trajectory problem becomes simple. Just one burn is needed from Low Earth Orbit (LEO) to escape and reach the Martian atmosphere. That burn results in a hyperbolic excess velocity (see the Keplerian Review Sheet) which, in vector addition with Earth's orbital velocity, gives the Mars Transfer Orbit injection velocity.

The angle between the hyperbolic excess velocity vector and the Earth's orbital motion vector matters. (see the figure) Only for the Hohman transfer orbit case does an angle of zero result in the minimum transfer time. If one is familiar with the "small angle approximation" this makes sense; one can "steal" a significant amount of outward velocity for very little penalty in total velocity by pitching out for the thransfer burn. This increasses the ∆v needed at Mars when you get there, but we'll use the atmosphere for that anyway. The resulting transfer orbit has a perihelion within Earth's obit and an aphelion outside of Mars' orbit.

Below, I've created a table based on a very simple Mars mission model. This considers Earth and Mars to be in coplaner circular orbits at their average distance and velocity from the Sun. For three dimensional, real-solar system complications, see one of the MERITT papers I did with the late Dr. Robert Forward, available on the Tether's unlimited web site (www.tethers.com). The below is only intended to give you an idea of the kinds of numbers and trades involved.

Table1. Earth to Mars Transfer Times

 ∆v km/s v(inf)  A rad  ∆t day  ∆v surf  ∆v LMO   ∆v capt  M tons |
-------------------------------------------------------------------
| 3.553 | 2.89 | 0.000 | 257.2 |  5.656 |  2.057 |  0.636 | 496.1 |
| 3.570 | 2.95 | 0.034 | 225.1 |  5.838 |  2.247 |  0.819 | 470.9 |
| 3.580 | 2.99 | 0.090 | 217.5 |  5.922 |  2.333 |  0.902 | 465.7 |
| 3.600 | 3.06 | 0.140 | 206.7 |  6.088 |  2.507 |  1.070 | 458.9 |
| 3.620 | 3.13 | 0.170 | 198.4 |  6.253 |  2.678 |  1.235 | 454.3 |
| 3.650 | 3.24 | 0.200 | 188.5 |  6.494 |  2.926 |  1.476 | 449.5 |
| 3.700 | 3.41 | 0.240 | 176.2 |  6.861 |  3.305 |  1.844 | 445.1 |
| 3.750 | 3.57 | 0.270 | 166.9 |  7.199 |  3.652 |  2.182 | 443.0 |
| 3.800 | 3.73 | 0.300 | 159.4 |  7.500 |  3.961 |  2.484 | 442.5 |
| 3.900 | 4.03 | 0.340 | 147.7 |  8.059 |  4.533 |  3.044 | 444.3 |
| 4.000 | 4.31 | 0.370 | 138.8 |  8.559 |  5.043 |  3.545 | 448.5 |
| 4.100 | 4.57 | 0.390 | 131.6 |  9.023 |  5.516 |  4.010 | 454.3 |
| 4.200 | 4.82 | 0.420 | 125.7 |  9.413 |  5.912 |  4.401 | 461.4 |
| 4.400 | 5.30 | 0.450 | 116.2 | 10.170 |  6.679 |  5.158 | 478.2 |
| 4.600 | 5.74 | 0.480 | 108.9 | 10.820 |  7.338 |  5.809 | 497.9 |
| 4.800 | 6.15 | 0.500 | 103.0 | 11.427 |  7.951 |  6.416 | 520.0 |
| 5.000 | 6.55 | 0.520 |  98.1 | 11.974 |  8.503 |  6.964 | 544.2 |
| 5.250 | 7.02 | 0.530 |  92.9 | 12.651 |  9.186 |  7.641 | 577.2 |
| 5.500 | 7.47 | 0.540 |  88.5 | 13.273 |  9.814 |  8.264 | 613.4 |
| 5.750 | 7.90 | 0.540 |  84.7 | 13.893 | 10.438 |  8.884 | 652.8 |
| 6.000 | 8.32 | 0.540 |  81.4 | 14.478 | 11.027 |  9.470 | 695.5 |
| 6.250 | 8.72 | 0.530 |  78.6 | 15.075 | 11.628 | 10.067 | 741.7 |
| 6.500 | 9.12 | 0.530 |  76.0 | 15.608 | 12.163 | 10.600 | 791.5 |
-------------------------------------------------------------------

A spacecraft starts from a 400-km LEO with the ∆v given in column 1 and coasts out to a "patch point" where it has the residual hyperbolic excess velocity with respect to the Earth given in column 2 and the pitch angle "A" given in column 3. Note that "A" is measured in the Earth's frame of reference with its "horizon" being a line perpendicular to the Earth-Sun radius. If our spacecraft were launched on a path directly away from the Sun as viewed from Earth, "A" would be 1/2 pi radians (90 degrees).

Vector addition of Earth's orbital velocity gives the transfer orbit injection vector, which is converted into Keplerian elements. The time of flight from the average radius of Earth's orbit to the average radius of Mars' orbit is calculated (column 4), along with the solar frame vector at Mars orbit crossing. This, is combined with Mars' average orbital velocity to give an inbound hyperbolic excess velocity with respect to Mars.

The periapsis of this inbound trajectory is set first at Mars' surface and second, at aerobraking altitude in Mars' atmosphere (taken to be 50 km) and the periapses velocities calculated. Column 5 gives the ∆v needed to arrive at Mars' surface without lithobraking. Column 6 gives the ∆v needed to achieve a circular Low Mars Orbit. Column 7 gives the minimum ∆v needed to achieve Mars capture (i.e., place the spacecraft in a highly elliptical orbit about Mars, just short of escape velocity at periapsis). In the last two cases, a small "circularization" burn will be needed as well to raise the periapsis out of the atmosphere; this has not been included due to laziness. Perhaps later.

Column 8 is an estimate of the initial mass in LEO of a vehicle to do this with a "dry" mass of 100 tons and an exhaust velocity of 3.5 km/s. It includes an estimate for consumables and protection of a crew of ten people at 31 kg per person-day (an international space station number). Note that the total mass declines as ∆v increases until 442.5 tons is reached, then goes up.

This particular number is not as important as the fact that there is a minimum. By carrying a little more fuel than needed for the minimum energy transfer, the transit time is reduced and the associated mass of consumables is reduced by more than the mass of the additional fuel. Indeed, under this model's assumptions, a trip time of 108 days can be made for the same initial mass as a Hohmann trip time of 257 days, reducing radiation exposure, "standing army" time back on Earth, along with other risks and costs of extended spaceflight. This is why astronauts will never fly to Mars on a Hohman transfer orbit, or even close to it. Look for journeys of 3 to 5 months from Earth to Mars, not 6 to 9 months.

G. Nordley, 2006