Planet Spacing and Insolation Habitability Zones

Most of our nearest neighbors are main sequence stars of spectral class M, commonly called "red dwarfs." These stars are less massive, less luminous, and less hot than stars like the Sun, but far more numerous. It used to be thought that because the distance of Earth-like insolation and the range around it scales with the luminosity of the star, one would be more likely to find planets in the wider habitable zones of bright, sun-like, stars. But planets tend to sort themselves out by orbital period ratios, not physical space, and those ratios get closer together as you get closer to the star. The net result is that red dwarfs like Gliese 876 are just as able to have multiple planets in their habitable zones as the Sun.


Radial width of insolation ranges as a function of stellar mass.
This chart used the Mass-Luminosity relationship in Lang's Astrophysical Data

A "habitable zone" is, of course, more complicated than a simple range of insolations. For one thing, redder light is more effective at heating and so the "habitable zone" for red dwarf planets lies somewhat further out from the star than a simple calculation of insolation might indicate. Also, various calculations of such zones include a range of assumptions concerning planetary atmospheres, albedos, magnetic fields, etc. The point here is not that planets with 40% of Earth insolation are habitable and planets with 39% are not, but that as many planets might be packed into a given range of insolations around low luminosity stars as around high luminosity stars.


Math notes: If P is the period of a planet's orbit in years, M is the mass of the star in Suns, and a is the seimimajor axis in AUs, then:

   P = sqrt(a^3/M), or
   a = (M P^2)^(1/3) (1)

If L is the luminosity of a star in Suns, the insolation of a planet in terms of Earth's is:

   I = L/a^2, or
    = sqrt(L/I) (2)

We can eliminate a from these equations by equating the right sides of equations (1) and (2) and solve for insolation as follows:

   (M P^2)^(1/3) = sqrt(L/I)
   (M P^2)^(2/3) = L/I
   I = L/(M P^2)^(2/3)
   I = (L/M^(2/3))/P^(4/3)

For two planets orbiting the same star, the ratio of their insolations, I1 and I2, is given by the inverse ratio of their periods, P1 and P2, to the 4/3 power alone, the other terms canceling:

   I1/I2 = [(L/M^(2/3))/P1^(4/3)]/[(L/M^(2/3))/P2^(4/3)]
   I1/I2 = [1/P1^(4/3)]/[1/P2^(4/3)]
   I1/I2 = [P2/P1]^4/3

If the ratio of periods, P2/P1 is 2, then the ratio of their insolations is I1/I2 = 2^(4/3) Å 2.52 for any star (or, I2/I1 = (1/2)^(4/3) = 0.397).

The ratio of their semimajor axes is given by equation (1):

   a2/a1 = (M P2^2)^(1/3)/(M P1^2)^(1/3)
   a2/a1 = (P2/P1)^(2/3) (a restatement of Kepler's law)
   with P2/P1 = 2, a2/a1 = 2^(2/3) = 1.59

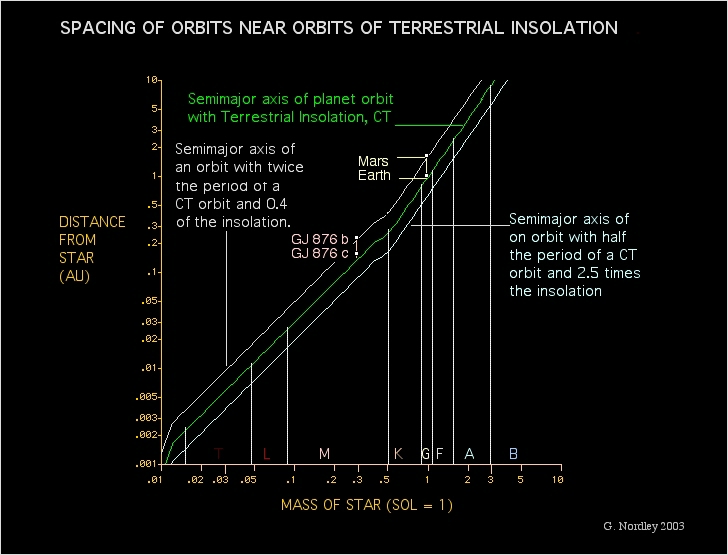
So, double the period of a one-Earth-insolation orbit orbit and the insolation goes down to 0.4, and the semimajor axis goes up by 1.6. If the I=1 orbit is 1 AU, the I = 0.4 orbit is 1.6 AU, but if the I = 1 orbit is 0.1 AU the I = 0.4 orbit is 0.16 AU.

---

Contact