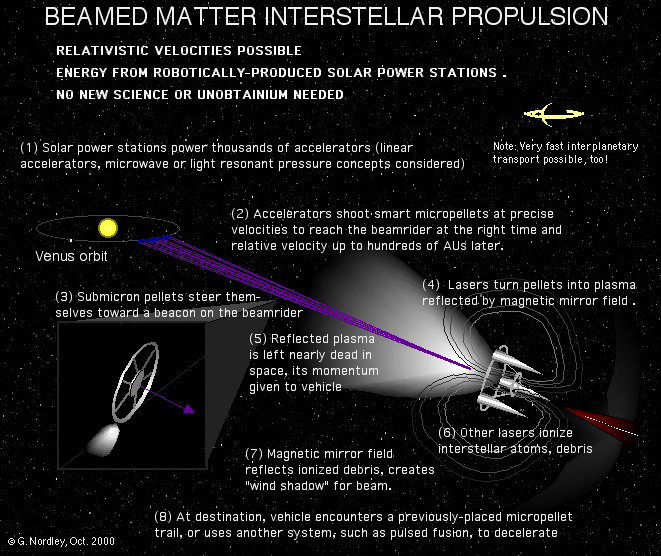
The Science Behind To Climb a Flat Mountain by G. David Nordley A. The Interstellar Propulsion System       The interstellar transportation system is the same mass beam propulsion concept I've used in all my future history, including The Black Hole Project series in Analog. The basics are laid out the illustration below. This illustration exists because Bob Forward once asked me to put the system on one chart, which he could use in his talks about star travel. One chart!? But Bob was a hard person to turn down. The wonder is not that the chart is a bit busy, but that it exists at all!

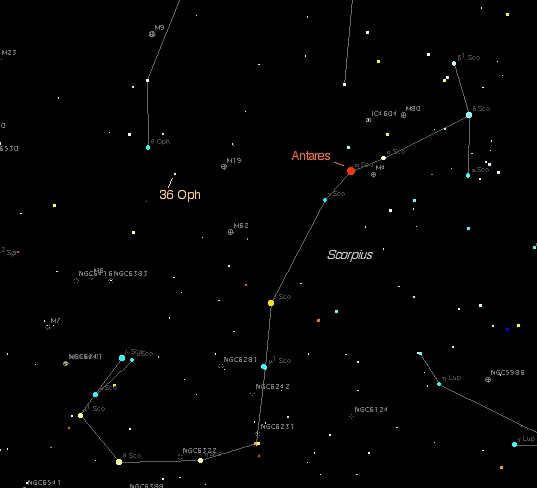
Some things should be emphasized:       (1) The main reason for any sail-based propulsion system is that the bulk of the mass of the propulsion system, and all of the unused fuel, doesn't have to be carried by the starship. This allows the starship to be accelerated for as long as a star has mass and energy. For instance, one can even imagine an intergalactic version powered by a Dyson Sphere.       (2) A mass beam, as opposed to a photon beam, can have its beam velocity programmed so that the reflected beam mass is left essentially dead in space relative to its beam drivers. This means that nearly all of the energy used to accelerate the beam is transferred to the starship. In a photon beam, much of the energy used to make the photons is carried away after reflection. Note that this difference becomes less important at high relativistic velocities, as the reflected photons are Doppler-shifted so far to the red that they contain little energy themselves. But most of the acceleration of a beamrider occurs at much lower velocities, where the efficiency advantage of a mass beam can be very significant.       (3) The particles or pellets of the mass beam need to be guided to their target by some means. I have posited that each particle is a tiny nano-missile (a "genius grain," if you like) that steers itself to the reflector on the starship aided by a beacon laser on the starship. Dr. Clifford Singer, in one of the first papers on pellet beam propulsion, posited guidance stations along the pellet route that use lasers to nudge any errant particles back into line. Powerful laser beams with an annular cross section have also been suggested. The particular steering mechanism isn't really important at this stage of speculative engineering; what is essential is that the particles are steered. If the vast majority of particles miss the starship sail, the efficiency advantage of (2) above is lost.       The version I've used posits a dual ring magnetic mirror for a sail. To use this, the particles have to be blasted into little plasma balls just before reaching the starship, which requires some clever future engineering. This, however, has a number of advantages over some kind of material reflector.       (1) It can be used as the nozzle for some kind of pulsed plasma auxiliary propulsion system. In my SF universe, the problem of detonating the nuclear reaction: B11 + H1 = 3He4 + energy has been solved, but there are many other possibilities.       (2) The fields can deflect any charged components of the interstellar medium ahead of the starship. A combination of lasers and electron guns can be used to ensure there are no uncharged components in the ship's vicinity.       (3) A small part of incoming plasma will leak through the central axis of the magnetic mirror, creating a magnetic shock wave in front of the ship which will also tend to deflect or at least slow ions in the interstellar medium.       (4) The combination of (2) and (3) above will create an extremely rarified "wind shadow" behind the starship for the incoming pellet stream to fly through.       Oftentimes, the first question people ask after encountering this system is "how do you stop?" The usual method would be for the ship to run into a previously placed stream of pellets/particles. This could be projected from the destination star, or from the Solar System a few years before the starship is launched. These streams would need to be kept collimated, of course, a task which I leave to the cleverness of future engineers. If the ship isn't going too fast, a pulsed nuclear fusion (Deadelus, Orion) could be used to slow down, perhaps in combination with drag from a "magnetic parachute," a much larger and gentler version of the magnetic mirror. Zubrin and Andrews described such a device for sailing on the Solar Wind in Analog a few years ago.       It was the question of 'what happens if the deceleration mechanism doesn't work?' which inspired To Climb a Flat Mountain. In this story, the ship is unable to decelerate at its intended destination and must try to find a place where its crew can survive that it can get to. The star map below show the location of 36 Ophiuchi as seen from Earth.

The gas clouds around Antares offer it a chance to use a "magnetic parchute" to lose most of its interstellar velocity and to reach a rare oxygen-atmosphere planet circling an ordinary red dwarf on the other side of the supergiant star. But when it reaches the gas clouds, they aren't quite as dense as predicted, and it's left with a little too much velocity. Even after a draconian shedding of non-essential mass, and using all its fuel in an optimum manner, it's left crashing into the planet's atmosphere at over 100 km/s.

B. Where are We?       Constellations are not places in space, but projections on our eyeballs of what lies in certain directions from Earth. Someone from "Orion" could be from as close as Ross 47, about 19 light years away, from Chi2 Orionis, over 32,000 light years distant, or from some distant galaxy in that direction, billions of light years away. A number of the bright stars in our sky are relatively near, such as Sirius, Vega, Altair, Alpha Centauri, Fomalhaut, and Procyon. These stars will shift position significantly in journeys of a few light years, rendering their constellations unrecognizable. Orion, however, is somewhat of an exception; its signature stars, those that form the shoulders, knees and belt, are about 700 to 1000 light years away, and so intrinsically bright that going another 600 light years only dims them by a magnitude and a half or so. By going in almost the opposited direction from Orion, parallax effects are minimized, and the constellation is, well, almost still recognizable, although now augmented by a number of the other stars in Scorpius, which have been passed by.in the journey toward Antares.

C. Low Gravity Worlds with Atmospheres       The astronauts of To Climb a Flat Mountain find themselves stranded on a world that is basically a "Warm Titan," with a few elaborations, of course. I'm not going to say too much about these elaborations until everyone's had a chance to read the first installment in Analog. However, there are a few points to make that shouldn't spoil people's enjoyment of the story.       The planet here orbits an old M2 or M3 red dwarf, cool enough to have little continuum ultraviolet radiation, but not so small as to be a flare star. It would be about a third the mass of the sun with about 1/30 the Sun's luminosity. The planet orbits at 27% of Earth's distance from the Sun and gets a Mars-like average insolation of about 0.43 of Earth's.       (1) One important requirement for atmosphere retention is that the molecular velocities at the top of the atmosphere (not the surface) be less than about a quarter of the escape velocity. This is relatively easy if the top of the atmosphere is cold enough.       I'm estimating the exobase temperature to be around 100K, but it could be lower. The escape velocity at the top of the atmosphere would be about 1.6 km/s and molecular velocity of nitrogen atoms at that temperature would be about 300 m/s. I have a formula for estimating the half life of an atmosphere based on exobase temperature and molecular weight which tells me that it would take about 3 trillion years for this planet to lose half its nitrogen by evaporation. Lighter gases like water vapor would be lost much more quickly; the same formula gives a half life of only 1.8 million years for that molecule. Water vapor, however, would never reach the top of the atmosphere; it would freeze out on the mountain sides.       (2) Another, and much more serious, concern is erosion of the atmosphere by the stellar wind. Old, early red dwarfs (M0-M3) are generally not flare stars and can be rather quiescent. They have significantly less mass loss and thus less stellar wind than the Sun, and also much less UV to create ions. However, 0.27 AU is really close and I suspect that a magnetic field will be needed to keep the stellar wind away from the atmosphere.       The tidal stress on this world is only slightly less than that on Mercury; however, it rotates in about thirty hours as opposed to 59 days. In the ordinary course of astronomical events, one would suspect this world would have a longer day. Setting that aside, the rotation period might be enough to generate a magnetic field if its core is still molten. However, its small size would argue that, if it were completely natural, the core should have solidified, so no dynamo. But clearly the atmosphere has not only not been blown away, but is very deep. It is thus natural for Jacques and company to suspect this world is not entirely happenstance.       These problems would go away, of course, if this world were in a one day or so orbit around a giant planet, such as Gliese 876b, with a friendly magnetosphere, like Saturn's. I didn't do that for a reason I never mention in the novel, and won't here until after the second part is published. At this point we know only that everything needed to preserve the atmosphere has happened.

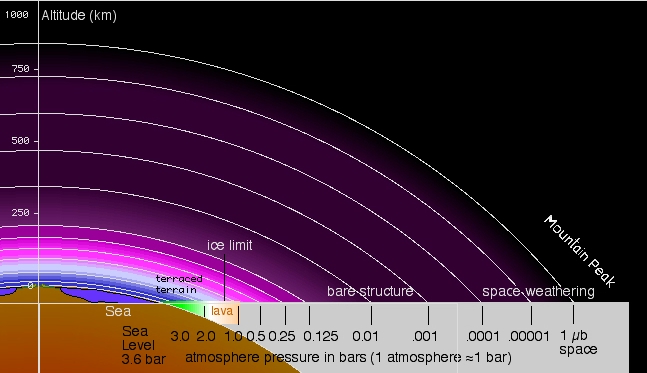How do we get tropical surface temperatures with Mars-like energy input? The answer is lapse rate. The effective temperature of a thick atmosphere planet is established where the atmosphere becomes transparent to outgoing infrared radiation. It can get really cold there, but for every kilometer one descends toward the surface, the temperature goes up. On Earth, it goes up about 6.5 kelvins per kilometer, on this world, a little less than one kelvin per kilometer.       But there are a lot of kilometers. With a surface gravity of about 1/7 of Earth's, it takes a column of air 7 times as deep to give one the same pressure. For a surface pressure of 3.6 atmospheres, that's about 25 times as much gas overhead as Earth. Taking into account changes in gravity and temperature as one ascends, air pressure doesn't get down to one atmosphere until one's climbed 87 kilometers above sea level. We need to almost double that for the stratosphere, where the effective temperature is established and the lapse rate starts. The stratosphere temperature is about 180 kelvins, sea level temperature, about 316.

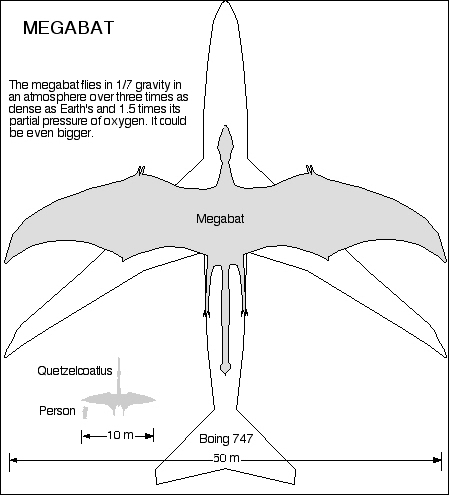
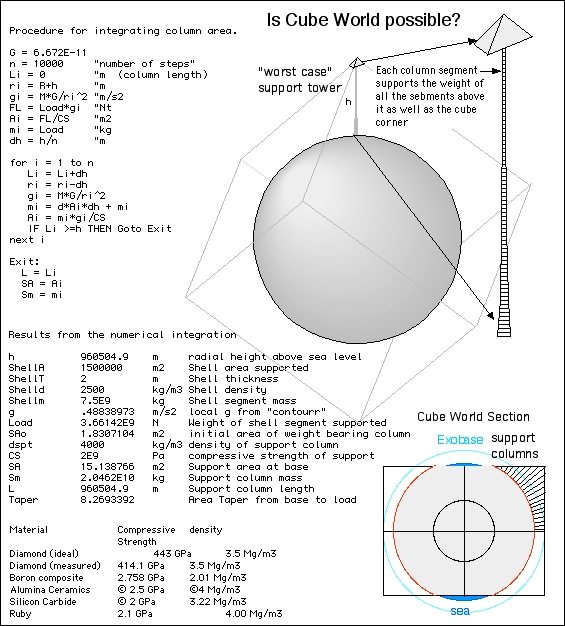
What's it going to look like? The view from the central caldera shown above goes out to over 2000 kilometers--no curvature to this horizon! We might expect a little distortion through the thick atmosphere, but remember that it gets thinner the higher one goes up the mountain slope. The distant view is highly forshortened of course. Surprisingly, rocks and shield volcanoes will look pretty Earth-like; while the biggest ones could get seven times as big, there's not room for (natural) volcanoes that big. Slopes of relaxation will look normal; the frictional force holding something back from a landslide goes down with gravity, but so does the force trying to make the landslide. The forces resisting compression or bending go up as the cross sectional area which goes up as the square of dimension. The mass of something goes up with the cube of dimension, but the force or weight trying to keep things in place goes down with gravity. If one keeps the proportions the same, it's a wash. Everything else being equal, structures at the limit of what the materials can support should get bigger by the factor that gravity goes down.       I've posited here that this will apply to structures of cellulose, bone and sinew as well. Before one goes too far in this direction, one needs to address the cube-square law. Take an Earth critter and make it seven times as large in dimension and it has 49 times the area but 343 times the volume, which means getting rid of 7 times the body heat per unit area that Earth critters do. To keep such critters viable, they need much lower metabolisms, an internal air conditioning system, a colder environment, or some combination of the above. Or maybe they just don't get quite as big as all that. Let evolution decide!       The megabats are a special case. If I scale the 12-meter wingspan of something like the pteranodon-like Quetzelcoatlus by a factor of seven for gravity, I get a wingspan of 84 meters. A 747 has a wingspan of about 60 meters, but it flies a bit faster and can use a higher wing loading. But wait, the atmosphere is 3.6 times as dense! Well, let's back off that to about three to account for the higher temperature. Based on wing loading alone, we could have a critter with a wingspan of something like 252 meters. That's two and half football fields. While it would weigh much, much less than a 747, or even 343 Quetzelcoatls, this gives us plenty of room to play with. We do need to cool the thing, and make it not so massively slow that it isn't a threat at all. I'm imagining the megabat as something the size of a small airliner, with plenty of room on its back for a few human mites. Rodan lives!

*****Spoiler Warning***** IF YOU HAVE NOT READ PART ONE, THIS REVEALS THINGS DISCOVERED IN THE COURSE OF READING PART ONE. FOR THE FULL EFFECT OF THE STORY, READ PART ONE FIRST. *****Spoiler Warning***** D. Planetary Shape      The world is, indeed, shaped like a cube. This strange shape is partly a result of its purpose, partly because of the star it circles and partly, perhaps, a bit of whimsey or the artistic sense of its builders. It is basically a luna-sized world with eight three-sided hollow pyramids spaced at equal intervals around the sphere. The mountains and the ridges between them isolate the six faces of cube world. Because the ridge lines are well above the level at which the atmosphere becomes transparent to infrared radiation (circa 0.1 bar), each face has its own effective temperature.

     Each face could have its own sea level as well, and its own surface pressure, but in practice, they are the same as on the alien builders' home world, whose evolutionary history cube world was built to explore. The mountain peaks jut above the exobase and their 30 K shaded faces provide a large are to "get" any volatile compounds in the atmosphere. Above a millibar or so, Cube World's atmosphere is mainly dry molecular nitrogen, mixed with a small amount of hydrogen flowing in from its star. Water, ammonia, and methane condense and return in this cold trap long before they are exposed to ultraviolet or solar wind.

     Here it would help to have a cube handy-a child's block or a cubical photograph holder will do nicely. Holds the cube in one hand by two opposite corners between the thumb and forfinger, straight up and down. The forfinger has the north pole and the thumb the south pole. Rotate the cube on this axis and observe that each face makes the same angle with respect to the line-of-sight to its center, as cube world does to its star. Thus the surface insolation (sunlight per unit area) is does not vary with lattitude. In the picture below, you are looking down on the north pole. The back is visible from Antares light and a faint aurora can be seen neer the pole on the dark face. We have here six physically identical biospheres, lit in the same way by the same sun. If each is seeded with the same primitive life forms, what will happen? What will evolve? One could possibly answer that problem with computer simulations more economically, but Cube World is more than a science experiment. It is a work of art, a reflection of stochastic biology playing against physical symmetry. For the builders of Cube World, sceince and art were not as seperated as they are on Earth.

E. Can Cube World Exist?

      While not in the class of Lary Niven's ringworld, Cube World is a huge structure. Is such a thing physically possible, even by a very advanced, and perhaps somewhat crazy to our way of thinking, civilization?
      I didn't have the time, nor expertise, to make a quantitative design for the entire world, nor did I teally need to do so; it is, after all, something conjectured to have been designed by aliens hundreds of millions of years ago, with techologies and experience we can only dimly project. What I thought I could do was to bound the problem, to satisfy myself that materials existed that were strong enough to support against its lunar-class gravity the envisioned shell structure that surrounds most of Cube World. What I wanted was to see if a tower strong enough to support the weight of the highest section of the shell and itself could be built out of diamond or other known materials. This requires an example, not an optimised design.
      What I did was to write a small program in a procedure window of TK! Solver that would numerically calculate the base area of each of ten thousand constant-pressure load bearing cylinders from the cube corner to the surface, given the tower's height, the local gravity and a marterial compression yield strength. Each cylindar is a little wider than the one above it, having to bear more weight at the same compressive strength. (Yes I could have used cone frustrums for more accuracy, but with 10,000 stepst, didn't think i needed it).
      The following is the result of a numerical integration from the corner cap down to the spherical surface, a distance of 960.5 km.(h)
      I used 2 GPa* We are already aware of several silica and composite materials that exceed that compressive strength, and if necessary one could wave one's hands in the direction of diamond, at 441 Gpa. Even structural diamond would be well within the capacities of the civilization that built Cube World--with significant margin.
      The pyramidal cap has a surface area of 1.5 E6 square meters and is modeled as a two-meter thick plate of material with a rock-like density of 2.5 tons per cubic meter. In practice, a thicker layer of less dense rock would likely be backed by a strong composite plate, but the overall mass should be a reasonable approximation. At a gravity of 0.5 m/s2 (at the distant corner of cube world) the corner cap weighs "only" 3.66 GN and at a strength of 2 GPa, would require a cross sectional area of 1.83 square meters to support it. The 1.83 square meters is the total load bearing area; in an actual design, this would probably be distributed through some kind of grid and transmitted to the main support column through arches.
      Each column section needs to support the sections above it as well as the load and gravity increases by a factor of three to lunar values as one goes down to the rock surface. The result is an tapered column with over twice the mass as as the load it supports. At 2 GPa, the column still has a relatively small footprint for a projected cap surface area of about a square kilometer of about 15 square meters at the surface.
      The columns "taper" is the ratio of the load bearing area of the column base to that of the top of the column supporting the surface, in this case about 8.3. Add in cross bracing, load distribution arches, plumbing and access tunnels and one still has fairly open interior structure, as described in the story.

 *Gigapascals. A pascal is 1 Newton per square meter. Giga is the standard System International prefix for billion. One atmosphere is about 100,000 Newtons, so 2 GPa amounts to about 20,000 atmospheres, or bars.

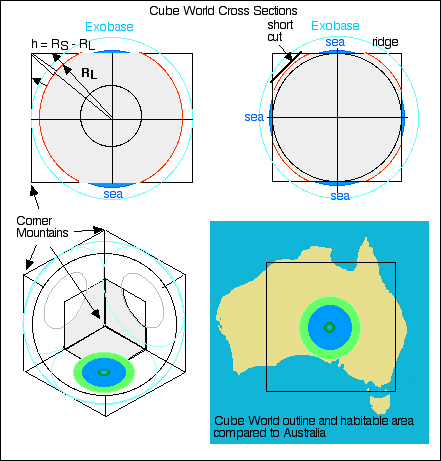Those interested may also wish to read: Robert M. Zubrin, "The Magnetic Sail," Analog, May 1992 G. D. Nordley, "Beamriders," Analog, July/August 1999. Jill Tarter et al., "A Reappraisal of the Habitability of Planets Around M-Dwarf Stars," in Astrobiology vol., no.1, 2007. R. McNeill Alexander, The Dynamics of Dinosaurs and Other Extinct Giants, Columbia University Press, 1989